数学徘徊記のほうで書いた競技数学の記事
なぜまとめたか?
数学徘徊記は競技数学以外の数学、本ブログは競技数学という感じで棲み分けしたくなったのでしました。
記事自体は移すつもりはありませんがリンクをまとめます。
競技数学に入るか入らないか微妙なものもあるんですが、ちょっとかすりそうだったら入れています。
記事(古い順)
2016年JJMOを受けてきた - 数学徘徊記
2016JJMO本選第4問 - 数学徘徊記
2015ジュニア広中杯の問題について - 数学徘徊記
円の反転とオイラーの不等式 - 数学徘徊記
等角共役点の証明 - 数学徘徊記
広中杯2016トライアル受けてきた - 数学徘徊記
広中杯2016ファイナル3問目 - 数学徘徊記
LTEの補題 - 数学徘徊記
マスターデーモンに挑戦 - 数学徘徊記
最近解いたEGMOの良問(2017年のEGMO日本代表一次選抜試験の問題2) - 数学徘徊記
傍心の有名な難問 - 数学徘徊記
2018JJMO本選模試 - 数学徘徊記
数学オリンピック対策用のリンク集 - 数学徘徊記
反転幾何まとめ - 数学徘徊記
2018JJMO本選模試 解答編 - 数学徘徊記
2018JMO受験記 - 数学徘徊記
2018APMO受験記 - 数学徘徊記
思ったこと
昔の記事を見ると恥ずかしくて初々しい気持ちになります。
IMO2022参加記
概要
2022年の7月に第63回国際数学オリンピックに参加しました。
公開が本当に遅くなりました! 終わってすぐ公開するつもりでしたがずるずると先延ばししてしまい、結局年末に書くことになりました。
会場はノルウェーでした。まだまだCovid-19が猛威を振るう中、3年ぶりに現地での開催となりました。
Observer Aとして参加し、問題の選定などの会議の参加、採点、coordination(主催者側の採点者と点数を話し合う会議)などを行いました。
時系列順に書こうと思います。
写真も貼りますが、写真速報と一緒に見るとより楽しめるかもしれません。 www.imojp.org
7/5
かなり余裕を持って成田空港に到着しました。
2019年のイギリス大会でも成田空港から出発したのですが(追記:そのときは羽田発でした!)、そのときより店が全然開いていないので、寂しかったです。
特にやることがなかったので、ウマ娘のイベントを消化していました。
そのあと団長団の皆さんと合流。来年の日本大会の視察もあるので、大所帯でした。
選手団より一足先に出発です。フィンランドのヘルシンキ空港経由でノルウェーのオスロ空港に向かいます。
クレジットカードを作っていなかったので日本円をノルウェークローネにする必要があるわけですが、思ったより取られますね…。約15円で1クローネが買えますが、1クローネは約11円にしかなりません。躊躇しましたが、いざという時のためにも30000円分交換しました。
夜はラウンジに入れました。軽く食事を取りながらチューター3人(僕、坂本さん、高谷さん)で雑談しました。ノルウェーの食事などをみんなで調べていました。ノルウェーの人口が550万人って少ないねという話をしました。
飛行機は快適でした。そもそも人が少なかったので、席を移動してゆったり座れました。機内食も美味しく、12時間ほどの長い航路でしたが映画のレパートリーがショボすぎることを除いて快適に過ごせました。
坂本さんと数学の問題を交換し(僕は複素関数論の問題を貰い、坂本さんに群論の問題を教えた)、少し考えたあと、ずっと寝ていました。
7/6
予定より早くフィンランドに到着し、2時間ほど時間があったので空港内を歩き回りました。ものすごくきれいな空港でした。

お土産を探しに回りました。トナカイの毛皮、ムーミンのぬいぐるみ(なぜかクオリティがアレなのもある)などなど。 書店にも行きました。なぜかキングダムハーツの2巻だけありました。クロスワードみたいなパズルがポピュラーらしいですが、あまりルールがわかりませんでした。 500mLのコーラが500円くらい。高いですね…。そもそも物価が高い+空港だから、という感じですね。
一通り歩いたあと、そのなかで一番お洒落そうだったカフェに行きました。高谷さんがタピオカの甘い飲み物みたいなスイーツを、坂本さんはチョコレートマフィンを買いました。僕は何も買いませんでした。
基本的にノーマスクです。みんなデカい。
飛行機を待ち合わせる場所でけん玉をやっていたらノルウェーの方に話しかけられました。夫婦とその娘さんの3人でした。けん玉のことや、これからIMOに向かうことなど、いろいろ話しました。父親は日本に来たことがあるらしく、東京に2週間位いたけど全然回りきれなかったと言っていました。
飛行機の中では高谷さんと数学の話をしました。高谷さんは大学院生で、ちょうど自分が興味を持っている分野を専攻しているため、どのようなことを勉強しているかとか、どのような勉強をしたらいいかなどを話しました。
飛行機から氷河地形が良く見えました。
オスロ空港に到着しました。ここもとてもきれいな空港でした。IMOのブースが出迎えてくれました。とはいえ特に何もない空港です。外に出るとかなり涼しく、羽織ったほうが良さそうな感じでした。一通り回って何もなかったのでIMOのブースに戻りました。高谷さんと坂本さんは将棋をしていました。僕はけん玉の練習をしていました。
そこからバスでドランメンへと出発です。IMOはオスロで開催されますが、問題選考会議などに参加する我々は、試験終了まで選手との接触を避けるために、ドランメンという隣町まで向かいました。オスロとは電車で1時間位離れた都市で、人口は約10万人です。
バスではずっと寝ていました。
ホテルに到着しました。それなりに良さそうなホテルでした。フロントマンがSpecialな部屋だと言っていて、ワクワクしながら部屋に向かうと、なぜか基本5階なのに1つだけ6階の部屋があるという感じで、
割と広めの部屋でした。相部屋ということで相手は誰か心配していましたが、坂本さんで安心しました。相部屋は誰か人によるらしく、高谷さんの場合はウズベキスタンの方でした(訂正:高谷さんから、カザフスタンの団長だったと連絡がありました)(その方はとても良い人だったとのこと)。
食事はビュッフェ形式でした。ノルウェーらしくスモークサーモンがありました。肉料理に加え、サラダなど野菜も豊富にありました。炭水化物はパンかジャガイモです。非常に美味しかったです。
そのあとIMO Shortlist(解答なし)を貰いました。Shortlistは来年のIMOまで公開を禁じられており、ここでこぼすとガチの国際問題になるため、何も言わないことにします。
みんなで少し問題を解いたあと、ショッピングモールに向かいました。IMO中は観光できるかわからないため、今のうちにお土産でも変えたらいいなと思い3人で出発しました。
洋服店が多いですが、書店や子ども用品、キッチン用品、家具屋が多い印象です。北欧らしいです。書店にはボードゲームも多く置いてありました。
一通り回りましたが、よくよく考えたら普通のショッピングモールにお土産らしいお土産はないか…。 ショッピングモールを出たあともドランメンを歩きました。教会に向かったり、ビール工場に向かったり(両方閉まっていた)しました。 ショッピングモールの外の店も入ってみたのですが、スーパーが一番楽しいかもしれません。輸入品が多い印象でした。スーパーで現地の食べ物をお土産に買っていきました。店員さんがカジュアルに腕にタトゥーを入れていました。お釣りをもらって驚いたのですがノルウェーの硬貨にも穴が空いていました。日本だけではないんですね。
輸入品の店もあり、もちろん日本の調味料もありました。「ポケ醤油」という見慣れない物がありました。 部屋に戻って調べてみると、ポケ(ポキ)というハワイの魚介類を使った料理があるそうです。知らなかった…。
橋の工事をしていました。ホテルまで音が聞こえました。部屋が揺れてる気がするのは気のせい?
夕食も非常に美味しかったです。


7/7
朝食も美味しく、たくさん食べてしまいました。 焼きサーモンは日本の焼鮭の味。焼鮭はやっぱり焼鮭です。 いろいろな種類のチーズがありました。

朝食の後Shortlistの解答をもらいました。少しみんなで読んだあと、僕はその後疲れて寝てしまいました。坂本さんや高谷さんはその間散歩に行き、カフェとか博物館とかに行ったそうです。
朝食を食べすぎて昼食はあまり食べられませんでした。
昼食後から怒涛の会議ラッシュが始まります。Shortlistの中から「この問題がいいと思う」みたいなのを言い合う会議があり、各国の意見を聞くわけですが、やはり人によって意見は違うんだな~と思いました。自分たちは嫌いだけど他は好き、みたいなことが多々あります。
ホテルに付いたときドリンク1杯と交換できる券を日数分貰っていたので、ビールを飲みました。お酒は少量だったら全然飲める体質でよかったです。お酒の違いはわからないですが、美味しかったと思います。
7/8
朝起きてTwitterを見たら安倍前首相が銃撃されたとのニュースが。そんなのノルウェーで聞かれても困るというか、実感がわかないというか…。日本にいても実感ないんだろうな。イギリス大会のときも京アニが燃えたのを思い出しました。
この日は朝から晩まで会議づくしで大変でした。英語を朝から晩まで聞いているわけですからね…。
会議でGeoffさん(IMOのリーダー)に日本の件について心配されたり、エレベーターで会った海外のObserverに日本の件について心配されたりしました。
IMOの問題が決まりました。とても簡単なセット(特に2番級)になったなと感じました。3番級も難しすぎることはないですし、日本選手に期待したいなと思いました。
夜8時位から散歩しました。オスロは日の入りがだいたい10時半なので、まだ夕方くらいの明るさでした。川沿いをずっと歩いていきました。 街の至る所で電動スクーターを見かけますが、思ったより速くてびっくりします。 apotekという名の付いた、緑の十字のマークの店をたくさん見かけました。最初はものすごく大手の店なのかなと思っていましたが、同じショッピングモール内に2つのapotekがあったり、複数の名前があるのを見ると、実はapotekは単に薬局という意味なのかもしれないと思いました。 カモメがたくさん飛んでいました。馬鹿笑いみたいな鳴き声でした。
ホテルに戻ってからはホッケーみたいなゲームをやりました。謎の才能を発揮しました。
7/9
午前中はIMOの問題の和訳をしました。問題1で人の名前をどうしようかと考えましたが、もとが女性の名前なので、副団長の名前でもある慶子さんにしようと考えました。
翻訳が終わって暇だったので、昼は3人で散歩しました。川と海の付け根部分にちょっとした島があったので、そこに向かいました。 砂浜に向かって靴を蹴り投げるチキンゲームを坂本さん一人でやったり、歩きながらイントロクイズをやったり、行き止まりの道を引き返したり、川に向かってダッシュしたり、いきなり鬼ごっこしたり、Ypsilon bridge(Y字形の橋)に行ったり、かなり歩きましたが、非常に楽しかったです。



夜は和訳について議論が紛糾し、とても大変でした。それが一通り終わった後、藤田さんに少し高いビールをおごってもらいました。いつものビールとは違うフルーティーな味でおいしかったのを覚えています。藤田さんの知り合いなどの世間話とか、馬主の話とかの話をしました。ビールは背の高いグラスになみなみと入っており、僕は大丈夫でしたが、坂本さんが全然まっすぐ立てないくらい酔っていました。
7/10
洋服をそこまで多くは持ってこなかったので選択したくなりましたが、聞いてみると水・木曜日しかできないらしく、手で洗うしかありませんでした。洗面台の栓がなかったので悩んだ結果ビニール袋を使用。絞るのは疲れました。
午前中の会議がなくなったため大学の課題をこなしました。
午後は開会式に参加するためオスロに向かいました。バスで1時間位でした。開会式の行われる前に人と話す機会は多かったのですが、あまり話しかけられず、反省しています。台湾のオブザーバーたちと会話しました。ずっとけん玉を練習していましたが、なんだか上達したような気がします。

開会式は選手たちは1階、団長団は2階に座り、接触がないように行われました。オスロ副市長など参加したほか、チューバやパーカッション隊の演奏などがありました。バックの音楽に合わせたピアノとチューバの演奏から始まり、ボーカルが男女2人入り、さらにラッパーが参加するというものがありました。盛り上がりました。
各国の選手が旗を持って1国ずつ紹介されていく たまに選手が1人だけの国があり、そのような国はものすごく盛り上がっていました。またウクライナも参加し、非常に盛り上がっていました。
世界の数オリができる600人が集まっていると思うとアツいですね。
北山選手が選手宣誓で出てきてマジか!となりました。
開会式の最後にビーチボール的なボールが10個くらい投下されるところがあり、みんなでバレーボールをしていました。たまに2階に上がってきて楽しかったです。
ベラルーシの方とけん玉で交流できました。けん玉をやってると勝手に向こうから話しかけてくるから非常に交流が楽です。けん玉を少しだけやったことがあるらしい。
夜は券が余っていたのでワインを2杯飲みました。クラクラしました。
7/11
午前中は何をしていたかおぼえていないですが、ゆっくりしていたか、会議をしていたのだと思います。
そのころ選手は試験1日目です。頑張れーー!!
午後は少し離れた別の大きいショッピングモールに向かいました。行きは初めてバスを使いました。物価の高いノルウェーにしては割とお手頃な料金でした。特に混むことはなく、普通のバスと言う感じです。
ショッピングモールでたくさん買い物しました。キッチン用品やタオルや調味料をお土産に買っていきました。カフェにも行きました。ミルクの割合が非常に大きいミルクコーヒーを飲みました。
そこからは歩いてホテルに帰りました。川沿いを歩いたのですが、ヨーロッパ風の景色で非常に見応えがありきれいでした。

夜は答案の採点をしました。日本選手は1・2を全員完答してそうで安心しました。沖選手の全完はあるかな、でも第6問難しいしな~という話をしてました。
7/12
試験2日目。さらばドランメン!静かで良い街で、ホテルもよかったので、名残惜しいです。
バスに乗ってオスロへ向かいました。途中でHolmenkollenというスキージャンプ台に寄りました。 あまり時間がなかったので頂上に行ったり展示を見たりすることはしませんでした。 お土産が売っていました。今までお土産らしいお土産を買う場所がなかったのでたくさん購入しました。こういうところで使わないでどうする。

オスロに到着しました。さすが首都という街並みで、洗練されていて綺麗でした。 昼食のタイミングで選手団と合流しました。4と5を皆完答している雰囲気で安心しました。簡単目の問題であっても落とさないということは難しいことです。
日本の選手と台湾の選手が仲良くしていました。京都大学に進学予定の台湾の選手とも合い、一緒に写真を撮りました。
RebelというIMO参加者のための交流施設があり、多くの選手がそこで遊んでいました。ボードゲームがたくさん置いていたり、卓球台やビリヤード台があったり、反射神経の対戦ゲームがおいてあったりしました。めちゃくちゃ楽しい施設で、このような施設はIMOごとに用意されるべきです。インドの選手たちとホッケーゲームをしました。
Rebelではそのとき講演会をやっていました(そのためにRebelに全員で来ていた)。内容はジャグリングと数学の関係についてで、日本だとピーター・フランクル氏がその話をしていた覚えがあります。
夜は採点です。採点の合間にけん玉をしていたのですが上達を実感しました。「ヨーロッパ一周」という技の成功率が凄く上がりました。
夜は神田さん・坂本さんと一緒にオスロを散歩しました。神田さんはすでにオスロを歩き回っていてよく街を把握しているため、案内される形で付いていきました。夜10時とか11時に散歩したのですが、高緯度のためそこまで暗くありませんでした。思ったより海がすぐそこでした。港を歩いて帰りました。
この日は1日がものすごく長かったです。


7/13
コーディネーションの会議がありました。私の参加したコーディネーションは大体高谷さんが話してくれた&あまり紛糾しなかったためかなり楽でした。特に第4問は会議もなく、向こうの方から「全員満点で同意したのでここにサインすれば大丈夫です」と話しかけられました。意外とコーディネーションは楽なのかな?と思いましたが、一方で神田さんと坂本さんの第5問はものすごく会議が紛糾しているようでした。
夜は高谷さんと2人で散歩しました。港に泊まっている船を外から見たり、丘に登ったりしました。特にこれといった目的もなくオスロの街並みを楽しみました。お笑いの話をしていました。


これはこの日の出来事だか忘れたのですが、Sushi Go!というボードゲームを日本のチューターと1人海外のスタッフで遊びました。なかなか楽しいゲームでした。スタッフの方は大学で日本語を少し勉強しているらしく、カードをシャッフルしていたら「速いですね~」と言われました。海外の人が日本語をしゃべっているのってなぜだか面白いです。
7/14
大人含めオブザーバー達でオペラハウスの方まで向かい、レストランで食事をしました。値段はやはり割高でした。味は割と普通?


そのあと神田さん・坂本さん・高谷さんと私でオスロを散歩しました。虎の像に登ったりしました。 そのあとお土産屋に寄ったのですが…店内で神田さん・坂本さんとはぐれてしまい、そこから2人ずつの別行動になってしまいました。 一旦Rebelに戻って少し遊んだ後、高谷さんと2人でまずオスロ市庁舎に向かいました。大きな壁画がいくつもある凄い建物です。ノーベル平和賞の授与式もここで行われているそうです。 そしてノーベル平和センターに行きました。ノーベルの人生や、過去のノーベル平和賞受賞者について展示されていました。英語でも説明されているので外国人にやさしいです。 最後は国立美術館に行きました。まず古代の美術から現代美術まで幅広く展示している、広くてきれいな美術館です。まず現代アートの方を見て回りました。どれもいろいろ訴えてくるものがあるので割と疲れますが良い展示でした。その後は近代の方に行きました。かの有名なムンクの叫びがあり、本当にあるんだなあって気持ちになりました。すでにいろいろ歩き回っていて疲れたので帰りました。

オスロを回ってみて、集約された街だと感じました。歩いただけでオスロの主要な観光地をいくつも回れたので、オスロの小ささを実感しました。(秋に東京に行ったのですが、改めて東京の大きさを実感しました。ヘルシンキ空港での会話をより理解しました。)
夜はお待ちかねのボーダー会議でした。オブザーバー達でボーダー予想をしていました。点数は伏せたまま人数だけでボーダー候補をいくつか提示され、人数比を考えてどのボーダーにするか決めるのですが… 銀と銅の間の人数が異様に多いのです。「これって28点なんじゃね?」「いやいや、いくら今年が簡単だからと言ってそんなことは…」「でも消去法で28点しかありえないよね」という話をしていました。 そしてボーダーが会議で決まった後は点数発表です。点数が発表された瞬間会場全体からどよめきの声が上がっていました。銀ボーダーが29点なのは異常です。宿泊するホテルに戻って、IMOのホームページを見ました。中国ヤバすぎ。日本は1桁順位と健闘していて嬉しく思いました。
7/15
表彰式です。神田さんと同室の人がコロナに感染したらしく、神田さんが珍しくテンション低めでした。後で陰性だとわかってほっとしました。 場所はオスロ市庁舎でした。私の時を思い出します。懐かしいなあ… 表彰式の後に次の年のIMOの紹介をするのがIMO恒例なのですが、来年は日本大会。ダサい動画を作ってないかかなり不安でしたが…悪くはない動画で安心しました。隣に座っていた藤田団長が英語で喋っていて面白かったです。 いろんな国の選手たちと一緒に写真撮影しました。特に中東の選手はトーブを着ており、すごく海外交流感がありました。
そのあとは全員でRebelに集合してパーティーでした。多くの選手と一緒に写真を撮りました。けん玉を披露したのですが凄く盛り上がりました。練習してよかった!
パーティーの終わった後はコンビニに寄りました。Tyrkisk peberを舐めたのですが、今まで食べたものの中でも本当にひどい味でした。ゴミに近い味がします。
コロナの検査をして全員院生が確認された後、みんなで帰国しました。
まとめ
総じて良い大会でした!
一番良かったのは遊び場所が用意されていたところでしょうか。
日本大会は大丈夫かな…?
サイト「ご注文は数オリですか?」を公開しました。
ご無沙汰してました。
タイトルの通り、サイト「ご注文は数オリですか?」を公開しました。
gochisuu.netlify.app
IMO日本代表経験者が集まって作ったサイトです。
ご注文はうさぎですか?のキャラクター達が数学オリンピックに挑戦するという設定の二次創作に加え、数学オリンピックの問題の「解いてみた」、また様々な話題を解説する記事など、様々な内容をご用意しています。
二次創作の構想は一昨年くらいからあり、サイトは今年の春から準備してきました。
まだ公開しているストーリーや解いてみたは少ないですが、今後更新していく予定です。
ぜひ見てみてください。
なお、こちらが公式Twitterです。
twitter.com
自作資料の共有フォルダ
作りました。
過去のJJMO本選模試やKAMOが入っています。
www.dropbox.com
数は少ないですが…
2019JMO代表選考合宿参加記 ~試験編~
dama-solved.hatenablog.com
の続きです.
ここにあるように代表選考の問題については一定期間公開が禁じられていますが, その期限が過ぎたため, 書けます.
問題はhttps://www.imojp.org/archive/mo2019/selection_camp/problems/2019.pdfにあります.
(今年から代表選考の問題がホームページに公開されたようです. 感謝. )
fuma-maple.hatenablog.com
を見て, そういえば書いてなかったし僕も書こうと思って書きました.
この記事と併せて読むのがいい気がします.
半年以上前のことを思い出して書いてるので, 間違ってるところがあるかもしれません. ご了承ください.
また, 問題のネタバレをされたくないひとは読まない方がいいと思います.
1日目
試験
問題をざっくり見る.
1問目はNで, 普通の問題感がある. 2問目は数列か…最近対策してきたしできたらいいな. 3問目はG. 一応自分の得意分野となってるし(←JMO予選もJMO本選もAPMOも0点のお前が何言ってんだ), 1問目をまず片づけて, 2問目と3問目を同時に考えていくか~
1問目はいろいろ頑張ったらできた. \(s\)が存在しない場合は簡単に見つかる. そうでないときは, \(n,k\)を素因数分解してわちゃわちゃやって\(s\)を構成する. 解答を書くの面倒くさいなあ. 使う文字の種類がかなり多くなった. 自分は解答を書くのに時間を使ってしまうタイプなのでこういうのは辛い.
で2問目と3問目を同時に考えていくか. とりあえず3問目の図を書く. 3番級でよくある3対称の難しい系かと思ったけど, 円が\(P\)で接することが予想できるし, 角度計算もしやすいし, 議論を進められそう.
というわけでいろいろangle-chaseをしていく. そして2ステップくらいで解けた. 3番級が解けたのは大きい. やったね.
と言っている間に同時並行で考えていた2問目, あまり進まない…よくわからない予想を立ててみたけど, その証明はできないし, その予想から本題も示せないし, なにやってんだ, という感じだった.
試験終了. やっぱりAは難しいね…対策が甘かった.
2日目
試験
4問目(1番級ですが, 2日目なので4問目になります)はFE. 足し算がない. あと\(\mathbb{Q}^+\rightarrow \mathbb{Q}^+\). まあ1番級なので焦らずやろう. 5問目はNで小問がある. そして6問目はC. ヤバそう. 6を捨てて4と5をやるか~
まず4問目. とりあえずいろいろ代入していったら, 任意の\(x\)において\(f(x)=f(y)^2\)なる\(y\)が存在することがわかって, さすがにずっとルートするのはヤバいので, 全部1. こういう問題を見たことがあったのでさっとわかった気がする.
5問目に移る. これに集中しよう. (1)と(2)のどちらかが成り立つことは証明できるのになあ~~~()
ここで, 良い数の相異なるものの和として表される整数を「まあまあな数」とする, 絶妙なネーミングセンスを発揮する.
さんざん格闘する挙句, まあまあな数があったとき, それから良い数をいろいろ引いたり足したりするとより小さいまあまあな数になることが分かった. これで(1)は解けた. あとは(2).
ここで(1)で使った議論を, 不等式評価を使って逆にやっていけば(2)もできることに気付く. やったー!
解答を書いて, もう数十分しか残ってなかったので, 6番の自明な構成っぽいものを書いた.
試験後
4問目は多くの人ができていたらしい.
5問目はあまりできた人が多くなさそうだった.
6問目はきおな氏だけが解けていたようで, 後ろでもチューター達が頭を抱え込んでいたらしく, 安心した.
しかも構成もやや非自明で, 自分の書いた構成は間違っていたらしい.
点数は7, 7, 0だった. 6問目の解説, なるほどな~, やはり組み合わせには厳しいものがあるなと実感した.
3日目
試験
7問目はC. 1番級のCって嵌ったら怖いやつだよなあ(←フラグ). 式もぎょっとするし. 8問目はG. さすがに解いておきたい. 9問目は多項式で, AかNかよくわからないけど, ステートメントが綺麗だなあってなった.
まずは7問目をやる. よくわからないので実験する. うーん, あまりつかめてこないし, むずそう.
8問目に移る. とりあえず図を書いて, やりたいことが見えてきたので補助線とか書いて…とやったら15分くらいで解けた.
多項式が好きなので9問目に手を付けてみたが, 考えれば考えるほどこれはヤバい問題だと実感した. どこから手を付ければいいのかさっぱり. 窮地に追い込まれた気分だった. 7問目を解かなきゃいけないのか~~
7問目で実験に実験を重ねるが, 全く手がかりが見えてこない. やばい…
8問目の解答を書いたり, 9問目でどうしようもない考察をしたりして気分転換をしながら, 7問目の考察をする.
そして2~3時間くらいたった後, ひらめきが下りてきた. これだ!!!
結局解答用紙の上半分に書いたとりとめのないことに大きく×印をして, そして証明は下半分しか使わなかった. こういう一発ゲーの問題, 思いつかないと辛いものがある.
9問目は何もわからない.
試験後
大荒れ. 7問目で嵌った人が少なくなかった. また, 8問目も実はそんなに簡単ではなかったようだったし, 9問目に至っては全然議論を進められた人がいなかったどころか, 分野もみんなわからなかった.
8問目はMiquel点を使っても解けるらしい. むしろそちらの方が多数派だった気がする.
試験前に演習でMiquel点が扱われたため, 救われた人が何人かおり, Miquel点がトレンドになった.
得点は7, 7, 0だった. まあそうだよね. 9問目はNだったらしい. 解説を聞いたがやはり難しい問題だと感じた.
IMOの代表に, 去年の1番級Aと今年の1番級C(この7問目)でともに嵌った人が2人いたため, IMO中ずっとネタにしていた.
4日目
今日は2番級Cがでるのか~. やだな~. という気分だった.
A, C, G, Nの4分野があるが, 4日全体で1番級, 2番級, 3番級に1分野ずつ出ることになっているので, 最終日はだいたい分野がわかる. 9問目のおかげで12問目の分野はわからないけど…
1番級Gをさっと解いて2番級か3番級を考えよう. という作戦だった.
試験
まず10問目に取り掛かる. さすがに5分で解けるやろ~~というナメくさった態度だった気がする.
あれ? あれあれ? ? なかなか解けない.
嵌ってる感あるな, ということで11問目に動く. ゲームで楽しそう. (1)はちょっと考えたらわかったけど, (2)についてはあまりわからないし, 難しいのかなと感じた.
12問目は面白そうだけど, あまり有効そうなことはできなかった.
10問目と11問目を行ったり来たりしていた. そのうちに10問目でうまい補助点を取ることができ, すっきり解くことができた. これいいなあ(一発ゲーだけど).
11問目に取り掛かる. 必勝法が思いつかないので, 小さい場合においてゲームの状態を全部書いてグラフを書いて, 脳筋で実験した.
そしてその実験が功をなして必勝法が見えた. 実験のおかげでかなり時間を使ってしまった(ここまで3時間半くらい?)が, 解けたのでヨシ!
12問目は, 虚無で解答用紙を埋めていた. ワンチャン部分点あるか!?という気持ち.
試験後
10問目も荒れていた. 一発ゲーは悲劇を生む…
11問目はみな出来が良かった. ずっと2番級Cで差がつくと思っていたので, 予想外だった.
12問目もみなあまりできていないようだった.
得点は7, 7, 0. さすがに12問目で虚無だけでは得点にはつながらなかった模様.
12問目は, 重要な関係式を2つ作る必要があり(1つはすぐ見つかるが, もう1つはなかなか見つからない), そこから次数下げをしていくと解けるということだった.
総合
56点. 全体としては上出来?
7点と0点しかなかったのも興味深い. 減点されない解答を書いたともいえるし, 部分点を全く取れなかったともいえる.
代表の中で最高点は62点, 最低点は45点.
京大理学部特色入試サンプル問題の雑な解説
雑な解説ですみません
問題
1
これはそんなに難しくない気がします.
(1)
最長の辺に注目すると, ほかの3辺の長さの合計がそれより大きくなることが必要十分なのがわかると思います. 必要性は明らかで, 十分なのは適当に構成できることからわかるはず.
(2)
\(AB+BC>CD+DA, BC+CD>DA+AB\)となるように\(a,b,c,d\)を\(AB,BC,CD,DA\)に割り当てられます。
こんな感じで辺を連続的に動かしていって, 対角の和が180°となるときが存在するのは中間値の定理を使えば示せます.

2
これもそんなに…?
(1)
(1)の問題文で出てきた事柄がその前に書かれた事柄に関係ないので, (2)の準備だろうなあってなります.
というかこれ積分の形のコーシー・シュワルツの不等式です. 知ってる人もいるはず…
任意の実数\(k\)において\(\int ^1_0 (|f(x)|-k|g(x)|)^2dx\geq 0\)となることを利用して, これは\(k\)の2次式(追記: \(k^2\)の係数が0になることは別個処理)なので, 判別式を見るとなんとこれが示せます.
(2)
(1)を使うことを考えます. また\(\int^1_0 dx/f^2\)の値が設定されてることもヒントにできます. ここまでヒントが与えられたら…という気持ちです.
3
これ思いつかないとつらいですよね. All or Nothingな問題な気がします.
例えば\(a_n={\rm ord}_2(n)\)(ただし, \({\rm ord}_2(n)\)で\(n\)が2で割れる最大の回数)とするとうまくいきます.
どうやって思いつくかっていう話なんですけど, 自分の場合, 周期的でないためちゃんとイレギュラーな項がたまに出てきてほしくて, でも周期性っぽいものも持ち合わせている…と考えたら思いつきました. 慣れに依存しているところもあるんですが…
4
これは整数論に慣れていないとちょっと難しい気がします.
(1)
どうせ帰納法やろ~~ってなって, 実際それでいけます.
\(b_{n+1},c_{n+1}\)は\(b_n,c_n\)で表せるので, 初めのほうの項を計算して, いい感じに\(a_n\)で表す予想を立ててみて, 帰納法を回せばいけます.
(2)
はじめ(1)を使った方法を考えてみるのですがあまりうまくいかないので, これは別個で考えるのかな, となります.
\(p=a_m\)とおきます(自分の場合素数は\(p\)のほうが慣れてるので…)
\((1+\sqrt{5})^{p^2}\)の1の項と\(\sqrt 5\)の項(語弊があります, 答案ではちゃんと書きましょう)がともに\(p\)で割って1余ればよいです.
気持ちなんですけど, \(p\)乗の展開は\(\bmod p\)でやりやすいです. というのも\(1\leq i\leq p-1\)のとき\(p|{}_p{\rm C}_i\)なので.
\begin{eqnarray}
(1+\sqrt{5})^{p^2}&=&((1+\sqrt{5})^p)^p \\
&\equiv& (1+5^{(p-1)/2}\sqrt{5})^p \pmod p \\
&\equiv& 1+5^{(p^2-1)/2}\sqrt{5} \pmod p \\
\end{eqnarray} と計算でき, フェルマーの小定理を使えば(2)も示せます.
(3)
いよいよ(2)を使いそうです. 数列の周期に注目するとできそう.
重要な考察なんですけど, \(a_1,\dots,a_{m- 1}\)は\(p=a_m\)の倍数でないので, \(a_m\)は\(p\)の倍数になる初めての項ということができます. これを使えばできます.
参考1
これは難しいです. たぶんサンプル問題・参考問題全6問の中で一番難しいです.
問題文は長いですけど読んでけばイメージがつかめると思います.
重要なこととして問題の操作は可逆です.
なので問題をシンプルにするために, 任意のパスを, 操作を繰り返してまっすぐにすることを考えます. これが可能だと示せたなら, 任意のパスを\({\bf A},{\bf B}\)とするとき, まっすぐなパスを\({\bf I}\)とすれば\({\bf A\rightarrow I\rightarrow B}\)とできるためOKです.
なんとなく, 先っぽからほどく感じでいけばできそう…と思うのですが, 図みたいにぐるぐる巻きにされているのもありなので, この方針だとつらいなあってなります.

でいろいろ実験してみて気づくのですが, 終点が右上の角にない場合は, 図のように, 終点からたどって一番右(もしくは上)にくるまでの部分を左右(上下)逆にするという操作をできることがわかります. この操作をAとします. そしてその操作によって縦の長さと横の長さはどちらかが増加するので, この操作は無限に繰り返せず, よって終点が右上の角に持ってけるなあ, ってなります. 右上に来た場合は図のように最後の曲がり角のところでまっすぐにできます. この操作をBとします.

しかしまだ解答にはたどり着かないです. 操作を終えられるかわからないし, 操作の回数については全然です…
というわけで私はうまい量を探しそれに注目しました.
「縦の長さ+横の長さ」と「曲がり角の数」に注目してみます.
すると「縦の長さ+横の長さ」は操作Aで必ず増加し, 操作Bでは変わらないか増加します(図参照).
(追記: 初めに、始点にいちばん近い曲がり角を第1象限にもってかないとそうならないですね. なので最初に持ってきましょう. 定数回で終わるのであまり影響しないです. )
またこれの最大値はパスの長さとなります.

「曲がり角の数」は操作Aで不変で, 操作Bで必ず1減少します.
これで操作の回数を評価でき, (1)と(2)が解けたことになります. (操作できない⇔パスがまっすぐ, なので)
全然言葉の定義をせずにここまで話しましたが, 答案では適宜言葉の定義をして論証を進めていきましょう.
2017 JMO 問2
Peingでリクエストがあったので書きます.
感想
昔解いたことがあるので解きなおしたんですけど, やはり自分の苦手なタイプですね…
JMO1~2番の中ではやや難くらいな気がします.
実験してみるとなんとなく成り立ちそうだなってのがわかるんですけど, それをどう証明すればいいのか…という感じの問題です.
解説
解いていくときの気持ち
問題文を見ます. 数列を定めていく問題らしいです.
まずは実験です. 適当に\(a_1,\dots,a_N\)を定めて数列を計算していきます. \(2^n\)で割った余りを考えるので2進数で数字を書いていったほうが見やすそう.
やってみると, ある\(n\)が存在し, 任意の\(i(1\leq i\leq n-1)\)において\(a_i< 2^n\)となると終わりだなってことがわかります. そういう項って\(n\)が大きくなっても余りは変わらないし. そうじゃない数列の要素がどうなっていくのかが問題の肝だなって気持ちです. それをどう扱おう…そういう項の集合を\(B_n\)とおいてみます.
やってみるとどうしても\(B_n\)の要素を\(2^n\)で割った余りがどんどん大きくなっていきます. でもちょっとやりにくいので数列全体で\(2^n\)で割った余りの最小値を考えてみます.
これが広義単調増加なのはすぐわかった. というわけで発散しないとすると有界ですね. この考え方はありがちです.
有界だと何がまずいんだろう…ちょっと悩みます. 考えてみると, 新しく出てくる項って絶対余りがそれより大きくなるので, \(B_n\)に入ってくれるものがなくなってくるんだなあってなります. そういうことを定式化してみます.
なんやかんやで解けた気がする…?解答を書くとき\(C_n\)を定めてみると書きやすいなあってなったのでそうしました.
解答
\(a\%b\)で\(a\)を\(b\)で割った余りを表すものとする.
任意の整数\(A\)において\(A\%2^{n+1}-A\%2^n\)は0または\(2^n\)であるためこれは常に0以上, すなわち\(A\%2^{n+1}\geq A\%2^n\)であり, また\( (2A)\%2^{n+1}=2(A\%2^n)\)となることに注意する.
\(n\geq N+1\)に対し\(c_n\)を\(\min(a_1\%2^n,a_2\%2^n,\dots,a_{n-1}\%2^n)\)と定める. このとき仮定より\(c_{N+1}\neq 0\)であり, \(n\geq N+1\)のとき\(a_n\)の定め方より\[a_n\%2^{n+1}=2((a_n/2)\%2^n)=2c_n\quad \cdots (1)\]である.
すると, 任意の正の整数\(A,n\)において\(A\%2^{n+1}\geq A\%2^n\)であり, また(1)より\(a_n\%2^{n+1}\geq c_n\)であるため, \(c_{n+1}\geq c_n\), つまり数列\(\{c_n\}\)は広義単調増加となる. 特に, 任意の\(n\)において\(c_n>0\).
また任意の\(n\geq N+1\)に対し\(c_n\leq a_1\%2^n \leq a_1\)よりこの数列は有界. よってある整数\(M_1\)が存在し, 任意の\(n\geq M_1\)に対し\(c_n\)は定数である. この値を\(c\)とする. \(c\)は数列\(\{a_n\}\)のある項を\(2^{M_1}\)で割った余りとなるため\(2^{M_1}>c\). また\(c>0\)である.
\(n\geq N+1\)に対し, 集合\(B_n\)を\(B_n=\{a_i|1\leq i\leq n-1, a_i\geq 2^n\}\)と定める. ある\(n\)が存在し\(B_n=\emptyset\)となるとき, \(a_{n+1},a_{n+2},\dots\)はすべて\(2\min(a_1,\dots,a_n)\)となるため題意が成り立つ.
\(n\geq M_1\)に対し\(C_n=\{b|b\in B_n, b\%2^n=c\}\)と定める. このとき, 任意の\(M_1\)以上の整数\(n\)において, \(d\in C_{n+1}\)のとき, (1)より\(a_n\% 2^{n+1}=2c>c\)であるため\(d\neq a_n\). \(2^{M_1}>c\), \(d\%2^{n+1}=c\)より\(d\%2^n=c\)である. よって\(d\in C_n\). したがって\(C_{M_1}\supset C_{M_1+1}\supset \cdots\)となる.
するとある整数\(M_2\geq M_1\), 集合\(C_{\infty}\)が存在して\(n\geq M_2\)のとき\(C_n=C_{\infty}\)となる.
これが空集合でないと仮定し, 任意の\(A\in C_{\infty}\)をとるとき, \(2^k>A\)なる整数\(k\)をとると, \(A\notin B_k\). よって\(A\notin C_k\)となり\(A\in C_\infty\), \(C_\infty \subset C_k\)に矛盾. よって\(C_{\infty}=\emptyset\)である.
すると\(n\geq M_2\)のとき, \(\min(a_1\%2^n,a_2\%2^n,\dots,a_{n-1}\%2^n)=c\)であり, \(a_1,a_2,\dots,a_{n-1}\)の中で\(2^n\)で割った余りが\(c\)となるものはすべて\(2^n\)未満であるため, \(a_n\)の定め方より\(a_n<2^{n+1}\)となる. よって\(a_n\notin B_{n+1},B_{n+2},\dots\)である.
すると, \(\max(a_1,a_2,\dots,a_{M_2-1})< 2^k\)となる\(k\)をとるとき, \(B_k=\emptyset\)となる. よって示された.
あとがき
解答としてどうだろう…
定義したものが多くて見にくい解答になった気がします.
まあしょうがない. そういうのをしっかり書く練習も重要な気がします.
数オリ財団の用意していた解答はもっと見やすかった気がします. そちらも見てみるとよいと思います.
これからもリクエストがあれば伝えてください.
この問題, どうしたらこのような発想が出てくるの?とか
解説に出てきたこの命題ってどうやって証明するの?とか
暇があったら書くかもしれません.
好きな問題いろいろ
やっぱり個人的に解いた問題もたまにはまとめなきゃと思うのでまとめます。
もともとこういうブログなので。
だいたいAoPSからコピーしてきたものなので和訳していません…
あとSLPなど有名どころが多いです。
文章・画像混ざっていますがごめんなさい。
A(代数)分野
数オリのAってぶっちゃけほぼ実数か有理数か整数なのですが。
2017 ELMO 6
Find all functions $f:\mathbb{R}\to \mathbb{R}$ such that for all real numbers $a,b,$ and $c$:
- If $a+b+c\ge 0$ then $f(a^3)+f(b^3)+f(c^3)\ge 3f(abc).$
- If $a+b+c\le 0$ then $f(a^3)+f(b^3)+f(c^3)\le 3f(abc).$
通信添削として出題された問題です。
難しいですがFEにしては変わった方法で解けるので好きです。
若干ヒントになるかも? 京大特色のおかげで解けた気がします。
2009 IMO 3
\(s_1,s_2,\dots\)は正の整数からなる狭義単調増加数列であり, \(s_{s_1},s_{s_2},\dots\)および\(s_{s_1+1},s_{s_2+1},\dots\)はどちらも等差数列である. このとき, \(s_1,s_2,\dots\)も等差数列であることを示せ.
さなさんにおすすめされたので解きました。いいですね~
3番級の中では簡単らしいですが結構時間がかかりました…
2013 SLP A5
Let $\mathbb{Z}_{\ge 0}$ be the set of all nonnegative integers. Find all the functions $f: \mathbb{Z}_{\ge 0} \rightarrow \mathbb{Z}_{\ge 0} $ satisfying the relation
\[ f(f(f(n))) = f(n+1) +1 \]for all $n\in \mathbb{Z}_{\ge 0}$.
これはまた特徴的な問題で…
結構難しいですが、解けた時の爽快感はかなりあります。
2014 和田杯 2

これも特徴的です。和田杯であることに注意。
こういうのをたまにやると数オリに毒される(?)こともなくなるかも。
2018 和田杯 11

有限集合っていいですよね(は?)
C(組み合わせ)分野
2012 SLP C3
In a $999 \times 999$ square table some cells are white and the remaining ones are red. Let $T$ be the number of triples $(C_1,C_2,C_3)$ of cells, the first two in the same row and the last two in the same column, with $C_1,C_3$ white and $C_2$ red. Find the maximum value $T$ can attain.
これはCというか…
2016 EGMO 3

ある量を上からor下から評価する問題の教育的な例な気がします。
2014 JMO予選 11

明らかに2項演算をわざわざマス目にした問題なんですけど、抽象代数っぽいことをすれば解けます。こういうのなかなかないので。
Sperner's theorem より
\(S_0=\{1,2,\dots,n\}\)の部分集合の属\(\mathcal{S}\)において、\(\mathcal{S}\)に属する任意の2つの異なる集合についてどちらかがどちらかを含むことはないとする。\(\mathcal{S}\)の要素数の最大値を求めよ。
自然な問題で、実はまあまあ難しいです。
割と好きなのでぜひ。
Sperner's lemma (2次元)
Given a triangle $ABC$, and a triangulation $T$ of the triangle, the set $S$ of vertices of $T$ is colored with three colors in such a way that
- $A$, $B$, and $C$ are colored red, blue, and white respectively
- Each vertex on an edge of $ABC$ is to be colored only with one of the two colors of the ends of its edge. For example, each vertex on $AC$ must have a color either red or white.
Then there exists an odd number of triangles from $T$, whose vertices are colored with the three different colors.
またSpernerさんですか…
これも好きです。
2017 SLP C2
Let $n$ be a positive integer. Define a chameleon to be any sequence of $3n$ letters, with
exactly $n$ occurrences of each of the letters $a, b$, and $c$. Define a swap to be the transposition of two adjacent letters in a chameleon. Prove that for any chameleon $X$, there exists a chameleon $Y$ such that $X$ cannot be changed to $Y$using fewer than $3n^2/2$ swaps.
競プロやってるひと得意そう。
2018 EGMO 3

これ面白い!!
2018 SLP C3
Let $n$ be a given positive integer. Sisyphus performs a sequence of turns on a board consisting of $n + 1$ squares in a row, numbered $0$ to $n$ from left to right. Initially, $n$ stones are put into square $0$, and the other squares are empty. At every turn, Sisyphus chooses any nonempty square, say with $k$ stones, takes one of these stones and moves it to the right by at most $k$ squares (the stone should say within the board). Sisyphus' aim is to move all $n$ stones to square $n$.
Prove that Sisyphus cannot reach the aim in less than
\[ \left \lceil \frac{n}{1} \right \rceil + \left \lceil \frac{n}{2} \right \rceil + \left \lceil \frac{n}{3} \right \rceil + \dots + \left \lceil \frac{n}{n} \right \rceil \]turns. (As usual, $\lceil x \rceil$ stands for the least integer not smaller than $x$. )
簡単ですが、ハマる人はハマります。
G(幾何)分野
2013 SLP G5
Let $ABCDEF$ be a convex hexagon with $AB=DE$, $BC=EF$, $CD=FA$, and $\angle A-\angle D = \angle C -\angle F = \angle E -\angle B$. Prove that the diagonals $AD$, $BE$, and $CF$ are concurrent.
かなり主張がきれいで、証明もいい感じです。
2002 SLP G7
The incircle $\Omega$ of the acute-angled triangle $ABC$ is tangent to its side $BC$ at a point $K$. Let $AD$ be an altitude of triangle $ABC$, and let $M $ be the midpoint of the segment $AD$. If $N$ is the common point of the circle $ \Omega$ and the line $KM $ (distinct from $K$), then prove that the incircle $ \Omega$ and the circumcircle of triangle $BCN$ are tangent to each other at the point $N$.
これはかなり難しいですが、主張も面白いしややきれいでいい問題だと思います。
2011 SLP G3
Let $ABCD$ be a convex quadrilateral whose sides $AD$ and $BC$ are not parallel. Suppose that the circles with diameters $AB$ and $CD$ meet at points $E$ and $F$ inside the quadrilateral. Let $\omega_E$ be the circle through the feet of the perpendiculars from $E$ to the lines $AB,BC$ and $CD$. Let $\omega_F$ be the circle through the feet of the perpendiculars from $F$ to the lines $CD,DA$ and $AB$. Prove that the midpoint of the segment $EF$ lies on the line through the two intersections of $\omega_E$ and $\omega_F$.
G3にしては難しいです。若干知識がいるかも…?
あまりないタイプな気がします。
2004 SLP G7
For a given triangle $ABC$, let $X$ be a variable point on the line $BC$ such that $C$ lies between $B$ and $X$ and the incircles of the triangles $ABX$ and $ACX$ intersect at two distinct points $P$ and $Q$. Prove that the line $PQ$ passes through a point independent of $X$.
教育的な問題です。
2012 SLP G6
Let $ABC$ be a triangle with circumcenter $O$ and incenter $I$. The points $D,E$ and $F$ on the sides $BC,CA$ and $AB$ respectively are such that $BD+BF=CA$ and $CD+CE=AB$. The circumcircles of the triangles $BFD$ and $CDE$ intersect at $P \neq D$. Prove that $OP=OI$.
バンジーさんの解いてみた集に載っていたので解きました。
主張がなかなか面白くて、手ごたえがあって良かったです。
2014 SLP G6
Let $ABC$ be a fixed acute-angled triangle. Consider some points $E$ and $F$ lying on the sides $AC$ and $AB$, respectively, and let $M $ be the midpoint of $EF$ . Let the perpendicular bisector of $EF$ intersect the line $BC$ at $K$, and let the perpendicular bisector of $MK$ intersect the lines $AC$ and $AB$ at $S$ and $T$ , respectively. We call the pair $(E, F )$ interesting, if the quadrilateral $KSAT$ is cyclic.
Suppose that the pairs $(E_1 , F_1 )$ and $(E_2 , F_2 )$ are interesting. Prove that $\displaystyle\frac{E_1 E_2}{AB}=\frac{F_1 F_2}{AC}$.
これもバンジーさんにおすすめされたので解きました。
点をどんどん言い換える感じ?で面白かったと思います。
2018 RMM 6
Fix a circle $\Gamma$, a line $\ell$ to tangent $\Gamma$, and another circle $\Omega$ disjoint from $\ell$ such that $\Gamma$ and $\Omega$ lie on opposite sides of $\ell$. The tangents to $\Gamma$ from a variable point $X$ on $\Omega$ meet $\ell$ at $Y$ and $Z$. Prove that, as $X$ varies over $\Omega$, the circumcircle of $XYZ$ is tangent to two fixed circles.
3番級ほどの難易度ではないですが、主張がきれいですし、面白いです。
N(整数論)分野
1987 IMO 6
Let $n\ge2$ be an integer. Prove that if $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le\sqrt{\cfrac n3}$, then $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le n-2$.
IMOの中ではかなり主張がきれいで有名な問題な気がします。
意外とやればできる問題でしたが、主張がきれいでポイント高めです。
H30年度 京大理学部特色 4

本質は(2)なんですけど、たぶんこの年の特色入試の中で一番難しくて面白いです。
2017 SLP N6
Find the smallest positive integer $n$, or show that no such $n$ exists, with the following property: there are infinitely many distinct $n$-tuples of positive rational numbers $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that both$$a_{1}+a_{2}+\cdots+a_{n} \quad \text{and} \quad \frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}$$are integers.
N6にしては簡単ですが面白いと思います。
2011 SLP N3
Let $n \geq 1$ be an odd integer. Determine all functions $f$ from the set of integers to itself such that for all integers $x$ and $y$ the difference $f(x)-f(y)$ divides $x^n-y^n$.
FE多くてごめんなさい…
教育的です。
IMO 2019 参加記 ~試験編~
試験の概要
体育館の中で試験をしました。
Contestant 1のブロック、2のブロック、…というように分かれていて、同じ国の人が近くに来ないようになっています。
トイレについては外に仮設のものが来ていました。誰がいつ出て入ったか管理されます。
Day 1 の感想
自分でも驚くほど調子が良かったです。
20分で(解答を書く時間含めず)問1と問2を解けてしまいました。
さっさとその答案を書き上げ、問3を考える時間を確保しました。
時間ギリギリでしたがなんとか問3を完答できました。
解説については https://www.imo2023.org/archive/mo2019/imo2019/problems/solutions-r856.pdf に書いてあるのでそちらを参照してください。
問題1
簡単だと思います。ちょっとやれば\(f\)が線形であることがわかるのでおわります。
問題2
ここでなんかめっちゃ天才になってました。公式のSolution 1と若干似ている解答です。
こういう共円ってその円上の補助点をとるといいことがあるよねってなって、謎な角度の条件を使えるように、直線\(BB_1\)と\(\odot B_1CP_1\)の交点をとったらすべてうまく行きました。
問題3
公式の解答とは違う若干めんどくさいことをしました。イベントを繰り返してどの頂点も次数が高々1にできるグラフは「良い」と言うことにするとき、橋のある連結なグラフは良いことをまず示し、次に最初の問題のグラフはイベントを繰り返して橋のある連結なグラフにできることを示しました。
橋のある連結なグラフが良いことの証明は、辺の本数の帰納法で、いい感じにイベントを起こすと帰納法が回ることを示す感じです。
最初の問題のグラフがイベントを繰り返して橋のある連結なグラフにできることの証明は若干大変ですが、適切にアルゴリズムに従ってイベントを起こすと、良くない状態(連結でないまたは完全グラフである状態)を回避しながら最終的に橋ができることを示す感じです。
Day 2 の感想
問4と5を1時間位で解いて、解答を書こうとして書いていったら問4で嘘をついていることがわかってやや悩んで、それであと試験が2時間位になった気がします。
問6は全然わかりませんでした…
試験後坂本君が「複素で行けた、頑張った」と言っていました。
問題4
簡単ですが若干面倒くさいです。2のオーダーと大小の比較で十分なのですが、自分は2のオーダーと3のオーダーを比べるという面倒くさいことをしてしまいました。LTEの補題とか出てきて大変です。
最終的に1点引かれていました。細かい部分で添え字を-1してしまったらしく、悲しいです。細かいミスにも注意しましょう。
問題5
簡単です。(b)で帰納的にできることは割とすぐに見えると思います。
問題6
本当に手がつけられませんでした。初等だとかなりきついと思います。
わからないですけど、解けている人はだいたい複素座標でしょうか…?
バンジーさんによる複素座標での解答です。
腕力💪 pic.twitter.com/SpDoF2FUDu
— バンジー (@kuronao0402) 2019年7月18日
IMO 2019 参加記 ~試験以外編~
7月13日
羽田まで
まだ学校はあるのですが、イギリスに行く準備をするために先に実家に帰省してから、羽田空港に行きました。父親もいました。
本当にドキドキです。
羽田空港
結構早くに付きました。JPN2と合流しました。
一緒にバンドリとかしてました。JPN2うまい…
結団式・直前学習会
通信添削というものがあって、代表6人は4回に渡ってIMO形式の問題を配られ、解答をチューターに送付し、添削してもらいます。(昔は代表候補全員やってたらしいんですけど…もうやらないのかな…)
第4回の添削の返却・解説がありました。
やはり「この部分は非自明だから説明したほうがいい」などいろいろ指摘されます。
第3回の添削でJPN6のしていた解法がヤバすぎてヤベえ(褒め言葉)ってなりました。組み合わせの問題を(マス目全然ないのに)マス目の問題に言い換えてそれを図形としてパップスギュルダンの公式を使う(は???????)らしいです。
飛行機
深夜のフライトになるため、飛行機に乗る前にラウンジに行けました。ご飯を食べました。
フライトは12時間位です。日本とイギリス(サマータイム)は時差が8時間あるため、ほとんど寝ていようと思っていましたが、そうはうまくいきませんでした。結局寝たのは6時間位でした。
翔んで埼玉を見ました。めちゃめちゃ面白かったです。
7月14日
ヒースロー空港
着いたー!!! 初ヨーロッパ、初イギリスです。
空港にIMOの受付会場がありました。
そこでミャンマーの代表と一緒に写真を取りました。
そこからバスでバース大学へと向かうのですが、あれ?? バスが見当たらない…?
しばらくしてスタッフの方が呼んでくれて助かりました。
バスで2時間位です。結構長い…
窓から眺める景色がとても綺麗でした。
バース大学
IMOの旗が立っていていよいよだなってなりました。
まずは宿泊施設に行きました。大学内の寮で、治安も環境も安心でした。

いくつか面白かったこと
- 自動ドアの開き方が開き戸
- エレベーターの音がうるさい
- カモメが多い

洗礼(昼食)
イギリス、前々からご飯が不味いって噂だったので心配でした…
からの
† JUST HAM †

衝撃的でした…
まじでハムしか挟まってません…
味はJUST HAMって味でした。
他の人は† JUST CHEEZE †とか食べてました。
その後
かなり暇でした。数学の問題を出し合って解いてました。
日没がめっちゃ遅いですね…時間感覚が狂います。
夕食
初めての食堂での食事でした。じゃがいも多くね?ってなりました。
やっぱびみょいですね。
WiFiが遅い…
7月15日
朝食
初めての朝食です。
食パンとクロワッサンとオレンジくらいです。
ココア(?)を飲みました…スイッチを押すと出てくるやつです…

※JPN5のツイートより
(`0言0́*)<ヴェアアアアアアアア
ココアの香りのするお湯って感じでした。砂糖を入れてなんとかしましたがひどかったです。
これが本場の味なの?とかなり疑問でした。
ココアの話はまた出てきます…
午前中
午前中もかなり暇でした。数学の問題を出し合って解いてました。
一発で解けるような問題を出し合ってました。
開会式

ホールで開会式がありました。
始まる前にDJがいろいろ曲をかけていました。
各国の入場がありました。
前々からトリニダード・トバゴをネタにしてきたので(代表選考でトリニダード・トバゴの問題にJPN5とJPN4がハマったので)トリニダード・トバゴを盛り上げました。
終わったあとにいろいろな国の選手と交流しました。インドの選手にけん玉を披露して鯉のぼりをプレゼントしました。
夕食
トマトソースのパスタを食べてみたけど…味付けが下手ですか???

※JPN5のツイートより
見た目よりもおいしくなくて、塩コショウをかけるとましになります。
桐間紗路生誕祭
おめでとうございます!!
7月15日はこの命が生まれた奇跡を全人類で祝うべきである(「ごちうさ」シャロ誕生祭をAbemaTVが実施 7月15日はこの命が生まれた奇跡を全人類で祝うべきである - ねとらぼ より)
Abemaのアニメ、イギリスから見れないようでした…悲しみ
7月16日
コンテスト
コンテスト1日目でした。コンテストの様子は別の記事で書こうと思っています。
午後
とりあえず頭がつかれました。タイムボムというカードゲームをやっていました。
7月17日
コンテスト
コンテスト2日目でした。コンテストの様子は別の記事で書こうと思っています。
午後
とりあえず頭がつかれました。
イギリスのスタッフである町野さんと会いました。高1らしいですが、日本語も英語も話せるし(通訳など大変お世話になりました)、すごい!
後で調べてみて知ったのですが、2019年EGMOで(イギリス代表として)金メダルをとっています。
町野さんに紹介されて、オーストラリアやイギリスの選手とカードゲームをしました。
Hanabiやmaoをしました。
Hanabiは競うのではなく皆である状態を目指す協力ゲームでした。なかなか難しい…
maoはかなり凶悪なゲームです。
en.wikipedia.org
まずルールを教えてもらえなくて、ルールを破ると指摘されてペナルティーカードをもらいルールを体得するという感じです。トランプを使うゲームで、原理的にはUNOと同じ(同じ数字またはスートの場合カードを出せ、カードを無くした人の勝ち)ですが、最初はめちゃくちゃカードを引かされます。
ゲーム外の内容を話すとペナルティというルールもあります(は??)
怒りとの勝負なゲームな気がします。
SETもしました。さすがIMO代表、ちょっと説明しただけですぐルールを分かってくれます…
そして近くの城?に行きました。丘の上にあったので景色が綺麗でした。
皆さんで集合写真を取りました。
JPN5が高熱を出し始めました。大丈夫でしょうか…
7月18日
京アニのニュースを知り悲しい気持ちになりました。
カナダの選手に京アニを心配されました。
Roman Bath

バースの有名な温泉の遺跡に行きました。イギリスには本当に温泉がないらしく、この温泉は貴重で、古代ローマ時代から文化的にも宗教的にも大切だったらしいです。
昔から建築技術がこんなに高かったのかと驚きました。
温泉の水を飲めるコーナーが有りました。
Comedy Walk
Comedy Walkというものに参加しました。ガイドさんがわかりやすく面白い解説をしながらバースの街を散歩するものでした。なかなか楽しかったです。
Fish and Chips

イギリスに来たということでFish and Chipsを食べました。
思ったよりはまずくなかったです。Fishはたしかに美味しかったです。
しかしなんでFish and Chipsなんでしょうか…FishとChipsがあって相乗効果もなにもないです。
とにかくじゃがいも好きですね。食堂でもずっとじゃがいもが出てきている気がします。
フリスビー
外国の選手などとしました。めっちゃうまいおじさんがいました。
7月19日
漫画(ごちうさのアンソロジー)を読んでいたら観光のバスで外国の選手に「なんの漫画を読んでるの?」って言われ、表紙を見せたら"Oh!! GOCHIUSA!!!"って言われました。ごちうさは世界を繋ぐ。
ごちうさは好き?って聞いたら、自分はそれほどではないけど好きな友人がいるとのことでした。
ストーンヘンジ

かの有名なストーンヘンジに行きました。
巨石が並んでいます。
現代でも何のために作られたかよくわかってないらしいです。しかし太陽の登る方角に関係があることから、天文学の知識があることは確からしいです。また石はかなり遠くから運んできたらしいです。
セルビアのガイドさんにお世話になりました。結構面白い人で、結構ムキムキでした。
また、ボスニアの日本語が話せる選手に会えました。5つくらい言語が話せるらしい。すごい…!
雨が降っていてとても寒かったです。
ソールズベリー

ソールズベリー大聖堂に行きました。非常に美しい教会でした。とても疲れていたので協会の中で寝てしまいました。ぐっすり寝られました。
マグナカルタを見ました。
CDとか買いました。
コンテストの得点
あるスプレッドシートに現在の自分の点数がリアルタイムで書かれているらしく、本当に心臓に悪いなと思いました。どの人も1つの問題の得点を非表示にされます。なので余計に心臓に悪いです。
Day 1 で満点を取れていると知り嬉しく思いました(特に問題3の満点は嬉しかったです)。
夜
夜はmaoを外国の選手としました。結構な国の人がいました。しかしmaoなのでほとんどゲームの内容しか口にしません。楽ですね。
結果発表
maoをしていたら途中でIMOの結果が出ていると報告を受けました。まっさきに結果を確認しました。
金メダルでした。本当に嬉しかったです。また他の日本の代表5人が全員メダルを取れていて嬉しかったです。JPN4も金メダルで嬉しかったです。
オブザーバーの方々も来ました。皆さんで集合写真を取りました。
7月20日
最も虚無な日です…
代表5人で「今日はJPN5が勝ち組だった」って言ってました。
Fermi Questions
ここはScience Olympiadではないですが、なんか企業主催のイベントでフェルミ推定をするものがありました。結果は普通でした。特にいい順位ではありませんでした。しかしみんなでワイワイ問題について話し合えて楽しかったと思います。
ハイキング(?)
虚無!虚無!虚無!虚無!虚無!
どこかの国のガイドさんのうるさいおばさんがいました。うるさいおばさんが「水がないとお前らのハイキングの保証ができない」というので急いで水を買ってきましたが、水が支給されました。クソ
そこからハイキング?が始まりました。どこに行くか全然知らないのでただただ従って歩いていくのですがなにか景色がいいわけでもなく何があるんだろう??っていう気持ちでした。うるさいおばさんが「時間がない、これはウォーキングではなくハイキングだ」ってうるさかったです。で気がつくと大学に戻っていた??ので本当に虚無でした。
講演会
バスに乗る前、うるさいおばさんが「バスが来たらみんな奥へ奥へ行け」ってうるさかったです。バスに乗ってからも「みんなは数学はできるかもしれないけどバスに乗ることすらできない、ただバスに乗るだけなのにできない」ってうるさかったです。
ベン・グリーンさんの講演会がありました。自分の目が悪かったのと、スライドの文字が小さかったのと、公園が英語だったのと、内容が難しかったことから、自分にはあまり理解ができませんでした…
カラオケ
僕とJPN1の2人で行きました。
これは楽しかったです。みんなで大合唱という感じでした。
DespacitoやLet it Goといった有名な曲は歌えたのですが、知らない曲も多かったです。歌えなくてもとりあえず乗るのが良いです。
ここで"I am a parallelogram"という曲に出会いました。中毒性がとても高く日本選手の中で話題になりました。
www.youtube.com
ココアリベンジ
JPN4がまずココアを恐る恐る注いでみると、とても濃いココアで、JPN4が「これマジで美味い」って言いました。次に僕が注いでみると、確かに濃いココアで、甘くてよく知っているようなココアでとても美味しかったです。次にJPN2が注ぎました。まだ美味しいものの味はそこまででした(もう?)。次に注いだJPN1は、もっと美味しいココアを知っていると、やや不評でした。次のJPN6となるともう今までのココアと同じでした。
美味しいココア、数杯でなくなっちゃうの?????
とはいえ機械の問題で安心しました。
このころからじゃがバターをすればいいことに気づきました。なんと気づくのが遅かったことか…!
7月21日
午前中
市街地に行ってお土産を買っていました。
表彰式

テントの下で行われました。移動遊園地が来ていました。なぜ?
映像でオブザーバーの村上さんと藏田さんがガッツリ写っていました。
表彰式では、1列ずつ呼ばれたあと(名前は呼ばれず、画面に映る)、メダルを各国のオブザーバーからもらい、自国の旗を胸の前で広げるといったことをしました。
そのあといくつか写真を取りました。
移動遊園地、結構絶叫アトラクションでびっくりしました。めっちゃ回ってました。
夕食はテント内に屋台やバンドが来ていました。昔のロックとかポップスを演奏していました。オブザーバーの先生に昔のロックに詳しい人がいて、色々とその話を聞いていました。
曲に合わせて踊っている人もいました。
その後
帰国のためのバスが深夜2時になるらしく、田崎さんに寝るなって言われました。なのでバスに乗ってからはめちゃ眠かったです。
もういよいよ帰国かあ~~
空港には極度乾燥(しなさい)のショップやYO!活があって面白かったです。
7月22日
7月21日と地続きみたいな感じなんですけどね(寝てないため)。
空港でみんな寝てました。
飛行機
giftedを見ました。リアルな内容だと思いました。
Hidden Figuresを見ました。かなり感動しました。
tedを見ました。かなりのくだらなさに笑いました。
小学生並みの感想…
7月23日
誕生日
JPN5の誕生日でした。前からこっそり書いていた誕生日カードをプレゼントしました。
日本
久しぶりの日本!!!!
暑い!!!!!!
表敬訪問
何も言うことを考えてなかったため、はじめまともなことをすべて言ってしまい、あとの人をかなり困らせました。本当にすいません。
その後
JPN1と一緒に神保町のエチオピアでカレーを食べたあと、書泉グランデでご注文はうさぎですか??の謎解きをやりました。難易度はやや簡単で、初心者に教育的な謎解きだったと思います。←今まで1回しかやったことがないくせに何言ってんだ
まとめ
ごちうさはいいぞ
いいぞ
真面目に
全体的に批判している感じになってしまいましたが、美しいバースの街並みの観光、選手との交流など、とても楽しかったです。これだけは言いたい。IMOは本当に楽しいので、中高生はぜひ目指してください。
今回始めてのIMOで金メダルをとることができ、本当に嬉しく思っています。
このIMOの体験すべてを将来の糧にしていきたいです。
LTEの補題(2)
su-hai.hatenablog.com
昔書いた記事ですが、何度か「これよりも簡単に証明できる」と言及されたので、(実質同じなんですけど)書きます。
\(x-y=kp^d\)とするとき、二項定理より
\[\begin{eqnarray}
x^n-y^n&=&(y+kp^d)^n-y^n\\
&=&ny^{n-1}kp^d+\frac{n(n-1)}2y^{n-2}k^2p^{2d}+Cp^{3d}\\
&=&p^d\left(ny^{n-1}k+\frac{n(n-1)}2y^{n-2}k^2p^d+Cp^{2d} \right)\cdots ☆
\end{eqnarray}\](\(C\)は整数)である。
- \(\mathrm{ord}_p n=0\)のとき
☆より、\(p\mid \hspace{-.67em}/n,y,k\)であることに注意すると、\(\mathrm{ord}_p(x^n-y^n)=d\)を得る。
- \(n=p\)のとき
☆より、\[x^p-y^p=p^{d+1}\left(y^{n-1}k+\frac{p-1}2y^{n-2}k^2p^d+Cp^{2d-1} \right)\]であるので、\(\mathrm{ord}_p(x^p-y^p)=d+1\).
- 一般のとき
\(\mathrm{ord}_p n\)についての数学的帰納法。\(\mathrm{ord}_p n=0\)のときについてはもう示した。\(\mathrm{ord}_p n=k\)のときに成り立つとし、\(\mathrm{ord}_p n=k+1\)のときについて考える。\(x\equiv y \pmod p\)より\(x^p\equiv y^p \pmod p\)であるので、
\[\begin{eqnarray}
\mathrm{ord}_p (x^n-y^n)&=&\mathrm{ord}_p ((x^p)^{n/p}-(y^p)^{n/p})\\
&=& \mathrm{ord}_p (x^p-y^p)+\mathrm{ord}_p (n/p)\\
&=&d+k+1
\end{eqnarray}\]であるので\(\mathrm{ord}_p n=k+1\)の場合も成り立つ。
以上より、LTEの補題が示された。
P.S. LTEの補題の証明は数オリでは必要なさそうです。
P.S. やはり必要らしいです、代表選考とかでは時間がない場合はいいけどあるのなら書くべきと先輩に言われました
数学オリンピック日本代表になりました
数学オリンピック日本代表になりました。
国際大会に向けて頑張ります。
今後もよろしくお願いします。
2019JMO代表選考合宿参加記
代表選考合宿について
春休みごろ行われる、数学オリンピックの日本代表を選考するための合宿です。
6人が日本代表に選ばれます。
JMOで優秀賞以上、JJMOで銀メダル以上を獲得すると参加することが出来ます。
ただし、新高3、つまり高2までがこの選考に参加することが出来ます。つまり私にとってこれが最後です。
そのほかにも、過去の日本代表が主であるチューターさんたちが参加します。
試験の形式は、IMOと同じ形式・ほぼ同じ難易度の試験を4日間行います。
1日3問4時間半です。
試験の問題については公開を固く禁じられているため(他国での代表選考にも使われるので)ここでは言えません。
感想とか手ごたえとかも危なそうなので言いません。
場所はオリンピックセンターでした。花見の名所です。
到着時は桜はまだ咲いていませんでしたが、合宿の終わりごろはかなり咲いていてとてもきれいでした。

1日目
表彰式がありました。そのあと開講式や自己紹介がありました。
去年も参加していたので、知っている人がまあまあいました。
今日は早く寝ました。午後8時。
2日目
ここからが本番です。
午前中は演習でした。チューターさんが問題やよく使われる考え方などを紹介するという形です。
今日は幾何と整数論でした。
幾何はMiquel点や回転相似についてでした。
整数論はいろいろな問題を扱う感じでした。最初の問題が mod 19 を用いる一発芸の問題だったので mod 19 が合宿のトレンドになりました。
試験 Day 1 でした。(さっき書きましたが感想は言いません)
夜はちょっと遊びました。数オリ界隈、SETがかなり流行ってます。
ja.wikipedia.org
みんなめっちゃ速くて怖いです。
でも試験があるので10時には寝る感じです。
3日目
午前中は今日も演習でした。
今日は代数と組み合わせでした。
代数もいろいろな問題を扱う感じでした。きおな君がとてもきれいな解法を発見してすげえってなりました。
組み合わせはかなり競プロでした(担当のチューターがyutaka氏だったので)。
試験 Day 2 でした。
4日目
午前中は講義でした。講義もチューターさんが行います。
グラフの隣接行列と固有値という内容でした。
普通はめっちゃ難しい内容をやって生徒がかなりおいていかれるという感じなのですが、今回は講義が親切で最後までついていけました。
グラフの問題を隣接行列の固有値に注目することで不定方程式をつくって頂点の数とかを絞るという内容で、とても興味を持ちました。
試験 Day 3 でした。
試験で疲れてゲームをする気力も起きなくなってしまったので、ずっと雑談などしてました。
あとJMOやAPMOの解答の見せあいもしました。
かなり楽しかったです。あと高1どうしのつながりが多くてすごいなあってなりました。
自分は算数オリンピックとか全く入賞したことがないのでね…
5日目
午前中は演習でした。
今日は特に内容は決まっておらず、チューターが何問かおすすめの問題を紹介して解説するという形でした。
試験 Day 4 でした。
立食会がありました。ビンゴ大会などがありました。
景品で「タイムボム」というカードゲームをもらいました。
試験がすべて終わったので夜更かししてみんなで遊びました。
もらったタイムボムを早速遊びました。
爆弾を爆発させたい陣営とさせたくない陣営がいて、誰がどの陣営か分かっておらず、心理戦をしながらさぐって自分の陣営の勝利を目指すという感じのゲームです。
人狼みたいな感じですが、ルールがとてもシンプルで、かつ奥深く、脱落者も最後まで出てこないので、とっても面白かったです。
6日目
今日は閉講式を手早くやってすぐ解散という感じでした。
まあ夜更かししていたのでぐったりとしてました。
せっかく東京に来たので初めての二郎に行きました。
とても美味しかったです。

全体を通しての感想
やはりメインは代表選考試験なので疲れます。
でも趣味の合う人たちと沢山話せるので楽しいです。
あとは結果を祈るだけですね…
2019 JMO 本選 問1~4 解説 (追記:問5)
全体の感想
難易度は1<2<3<4<5だと思いました.
問5はまだ解けていません…
(追記: 解答を載せました(自力ではないですが))
問1
略解
\(b\)と\(c\)の大小で場合分け.
・\(b=c\)のとき
\(a^2+b+3>0\)より解なし.
・\(b>c\)のとき
\(a^2=(b^2-c^2)^2-b-3<(b^2-c^2)^2\)
\(b>c\geq 1\)より\(b^2-c^2\geq 1\)であり, \(a^2,(b^2-c^2)^2\)はともに平方数なので
\[\begin{eqnarray}
(b^2-c^2)^2-b-3&\leq&(b^2-c^2-1)^2\\
- b-3&\leq&-2(b^2-c^2)+1\\
b^2-\frac b2-2&\leq&c^2
\end{eqnarray}\]ここで\(b>2\)のときは\[(b-1)^2< b^2-\frac b2-2\leq c^2\]が成り立つが, これは\(b>c\)という仮定に矛盾. よって\(b\leq 2\)である. この場合は\((a,b,c)=(2,2,1)\)のみ.
・\(b< c\)のとき
さっきと同じような感じで解くと解がないことがわかる(やってみてください).
問2
感想
1回1回得点が入るのが面倒臭いですね…
これもやればできる問題だったと思います.
記述がちょっと大変そう?
略解
\(\pmod n\)のみが本質のため1を\(n\)個, 2を\(n\)個, ... , \(n\)を\(n\)個書くとしてよい.
各行・列に注目したときの, 「その行・列で総和が変更されてそれが\(n\)の倍数となる回数」をその行・列のスコアと呼ぶことにする.
最終的な得点は, 各行・列のスコアの総和に等しい.
ある行に注目するとき, 最終的にその行にかかれる数の総和が\(S\)ならば, 書かれる数がすべて正であるため, その行が\(n\)の倍数になる回数=スコアは\([S/n]\)以下である.
\(i\)行目に書かれる数の総和を\(S_i\)とするとき, 行全体におけるスコアの総和は
\[\begin{eqnarray}
\Big[\frac{S_1}{n}\Big]+\Big[\frac{S_2}{n}\Big]+\cdots+\Big[\frac{S_n}{n}\Big] &\leq&\Big[\frac{S_1+S_2+\cdots+S_n}{n}\Big]\\
&=&\Big[\frac{n(1+2+\cdots+n)}{n}\Big]\\
&=&\frac{n(n+1)}{2}
\end{eqnarray}\]以下である. 列についても同様なので, 結局最終的な得点は\(n(n+1)\)以下.
得点を\(n(n+1)\)にすることが可能なことを示す. \(i\)行目, \(j\)列目のマスを\((i,j)\)と表すこととする. また, 任意の整数\((i,j)\)について\((i+n,j)=(i,j+n)=(i,j)\)とする.
以下の操作を\(k=n,1,n-1,2,\dots,\frac{n-1}{2},\frac{n+1}{2}\)の順に繰り返す:
マス\((0,k),(1,k+1),\dots,(n-1,k+n-1)\)に\(k\)を書き込む.
これで得点\(n(n+1)\)とれることの証明は略す(やればできるので…).
問3
感想
ちょっと簡単目の関数方程式だったと思います.
感覚でいろいろやれば解ける感じだったので個人的に楽でした.
略解
このサイトの解が結構きれいです.
JMO2019本選問3 | 凸レンズの部屋(仮)
問4
感想
解けませんでした…後輩から解説を聞きましたが解けるべきでした…
略解
図のように点を取る. \(DM=ME\)となるのは有名な構図.

すると\(\angle DGE=90^\circ\)より\(MD=MG\). よって\(MG\)は\(\omega\)に接し, \(\angle IG M=90^\circ\)である. すると四角形\(AHJM\), 四角形\(AHDG\), 五角形\(IDJMG\)はそれぞれ円に内接する. この3つの円の根心は\(K\)となるため, \(G,D,K\)は共線. \(AK//FD\)より\(GF:GA=GD:GK\)で, \(\odot AGK\)は\(\omega\)と点\(G\)で接する.
問5
感想
本番では何もできそうになかったので白紙でした(よくない)
略解
AoPSに今年のJMO5の問題文をpostしたら、見たところ正しそうな解答が返ってきていたので和訳してご紹介します。記述は全体的に端折ってますが簡単に埋まります。 pic.twitter.com/Zk3RKrvlAg
— maple (@fuma_maple) February 19, 2019
2019 JJMO 本選 解説
全体の感想
難易度は1=2<4=5<3な気がしました(あくまでも個人の感想です).
例年よりちょっと難しいくらいな気がします.
問題→第17回(2019年)JJMO 本選 の問題
解答で略している部分があります, すみません
問1
感想
ちょっと(1分くらい)悩みましたが, 30°なので外心をとってみるとなんかできました.
解説
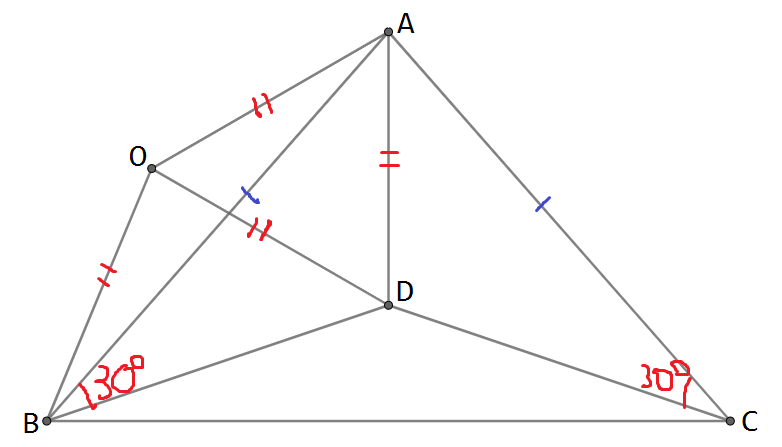
\(\triangle ABD\)の外心を\(O\)とするとき
\(\angle AOD=2\angle ABD=60^\circ\)より\(\triangle AOD\)は正三角形.
よって\(AD=OD\).
また\(\angle BOD=2\angle BAD=\angle BAC, OB:OD=AB:AC=1:1\)より\(\triangle BOD\sim \triangle BAC\).
すると\(AC:BC=BD:OD=BD:AD\).
よって角の二等分線定理より示された.
問3
感想
たぶん今回のJJMOの中で一番難しいと思います.
解説
(1) \(a+b+1=x\)とおくとき
\(\gcd(a,b+1)=\gcd(x,a)\)
\(\gcd(a+1,b)=\gcd(x,a+1)\).
背理法で示す.
\[\gcd(x,a),\gcd(x,a+1)>\frac{\sqrt{4x+1}-1}{2}\]と仮定して矛盾を導く.
\(a\)と\(a+1\)は互いに素より
\[\gcd(x,a)\neq \gcd(x,a+1)\]\[\gcd(x,a(a+1))=\gcd(x,a)\cdot \gcd(x,a+1)\]よって\(\gcd(x,a),\gcd(x,a+1)\)のどちらかは\(\cfrac{\sqrt{4x+1}+1}{2}\)より大きく
\[\begin{eqnarray}
\gcd(x,a(a+1))&=&\gcd(x,a)\cdot \gcd(x,a+1)\\
&>&\frac{\sqrt{4x+1}+1}{2}\cdot \frac{\sqrt{4x+1}-1}{2}\\
&=&x
\end{eqnarray}\]となるが矛盾.
(2)\(\min(\gcd(x,a),\gcd(x,a+1))=\cfrac{\sqrt{4x+1}-1}{2}\)は整数なので\(4x+1\)は平方数.
よって\(x=n^2+n\)(\(n\)は正の整数)とおける.
このとき\(\cfrac{\sqrt{4x+1}-1}{2}=n\).
\(\gcd(x,A)=n\)(ただし\(A=a\)または\(A=a+1\))なる\(A\)がある. \(B=2a+1-A\)とする.
\(\gcd(x,A)\neq\gcd(x,B)\)かつ\(\min(\gcd(x,A),\gcd(x,B))=n\)より\(\gcd(x,B)\geq n+1\)であるが\(\gcd(x,A)\cdot \gcd(x,B)=\gcd(x,a(a+1))\leq x\)より\(\gcd(x,B)\leq n+1\). よって\(\gcd(x,B)=n+1\).
\(\gcd(x,a)=n,\gcd(x,a+1)=n+1\)のとき, \(a=kn,a+1=l(n+1)(1\leq k\leq n, 1\leq l\leq n-1)\)とおける.
すると\(a=kn=ln+l -1\)だが, \(0\leq l -1< n\)より\(k=l\). すると\(k=l=1\)より\(a=n\)がわかる.
\(\gcd(x,a)=n+1,\gcd(x,a+1)=n\)のときも同様にすると\(a=n^2-1\)がわかる.
よって\((a,b)=(n,n^2-1),(n^2-1,n)\).
問4
感想
難しいような簡単なような…
いろいろな方法がありますが思いつかないと難しいでしょう(無難なコメント).
構成も意外と出てこなかったりしそうです.
解説
図のような感じで塗り分ける.

駒が通った道筋を辺とするとき
●から出た斜めの辺の本数=○から出た斜めの辺の本数
●から出た斜めの辺の本数\(\leq 2\times\)(●の数)=\(\cfrac{(n-1)^2}{2}\)
○から出た辺の本数\(\geq 2\times\)(○の数)\(-2\)=\(\cfrac{(n+1)^2}{2}-2\)
○から出た斜めでない辺の本数
=○から出た辺の本数-○から出た斜めの辺の本数
\(\geq\cfrac{(n+1)^2}{2}-2-\cfrac{(n-1)^2}{2}\)
\(=2n-2\)
構成は略します.
別解
こちらのサイトに別解と構成があります.
こちらのほうがきれいな感じがします.
JJMO本選2019問4 | 凸レンズの部屋(仮)
問5
感想
5番の割にはそんな難しくない気がします.
JJMO, なんで3年連続で5番にGをおくのでしょうか???
解説
学校の後輩が天才的な解法を見つけてくれたので書きます.

\(\odot AMC\)と直線\(AN\)の交点を\(P\)とおくと, 簡単な角度計算で
\(\triangle NHA\sim \triangle NMC\)
\(\triangle KAN\sim \triangle PCN\)
がわかるので
\(四角形KAHN\sim 四角形PCMN\).
すると対応する角度が等しいので
\(\angle AKH=\angle CPM\)
すると円周角の定理より
\(\angle AKH=\angle CAM\).

