2019 JJMO 本選 解説
全体の感想
難易度は1=2<4=5<3な気がしました(あくまでも個人の感想です).
例年よりちょっと難しいくらいな気がします.
問題→第17回(2019年)JJMO 本選 の問題
解答で略している部分があります, すみません
問1
感想
ちょっと(1分くらい)悩みましたが, 30°なので外心をとってみるとなんかできました.
解説
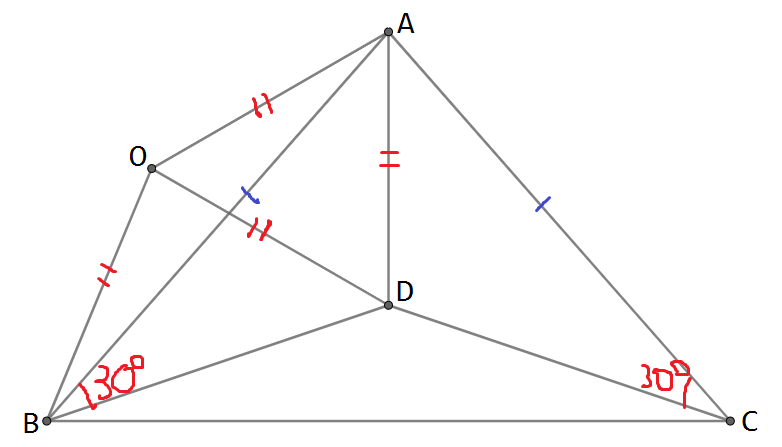
\(\triangle ABD\)の外心を\(O\)とするとき
\(\angle AOD=2\angle ABD=60^\circ\)より\(\triangle AOD\)は正三角形.
よって\(AD=OD\).
また\(\angle BOD=2\angle BAD=\angle BAC, OB:OD=AB:AC=1:1\)より\(\triangle BOD\sim \triangle BAC\).
すると\(AC:BC=BD:OD=BD:AD\).
よって角の二等分線定理より示された.
問3
感想
たぶん今回のJJMOの中で一番難しいと思います.
解説
(1) \(a+b+1=x\)とおくとき
\(\gcd(a,b+1)=\gcd(x,a)\)
\(\gcd(a+1,b)=\gcd(x,a+1)\).
背理法で示す.
\[\gcd(x,a),\gcd(x,a+1)>\frac{\sqrt{4x+1}-1}{2}\]と仮定して矛盾を導く.
\(a\)と\(a+1\)は互いに素より
\[\gcd(x,a)\neq \gcd(x,a+1)\]\[\gcd(x,a(a+1))=\gcd(x,a)\cdot \gcd(x,a+1)\]よって\(\gcd(x,a),\gcd(x,a+1)\)のどちらかは\(\cfrac{\sqrt{4x+1}+1}{2}\)より大きく
\[\begin{eqnarray}
\gcd(x,a(a+1))&=&\gcd(x,a)\cdot \gcd(x,a+1)\\
&>&\frac{\sqrt{4x+1}+1}{2}\cdot \frac{\sqrt{4x+1}-1}{2}\\
&=&x
\end{eqnarray}\]となるが矛盾.
(2)\(\min(\gcd(x,a),\gcd(x,a+1))=\cfrac{\sqrt{4x+1}-1}{2}\)は整数なので\(4x+1\)は平方数.
よって\(x=n^2+n\)(\(n\)は正の整数)とおける.
このとき\(\cfrac{\sqrt{4x+1}-1}{2}=n\).
\(\gcd(x,A)=n\)(ただし\(A=a\)または\(A=a+1\))なる\(A\)がある. \(B=2a+1-A\)とする.
\(\gcd(x,A)\neq\gcd(x,B)\)かつ\(\min(\gcd(x,A),\gcd(x,B))=n\)より\(\gcd(x,B)\geq n+1\)であるが\(\gcd(x,A)\cdot \gcd(x,B)=\gcd(x,a(a+1))\leq x\)より\(\gcd(x,B)\leq n+1\). よって\(\gcd(x,B)=n+1\).
\(\gcd(x,a)=n,\gcd(x,a+1)=n+1\)のとき, \(a=kn,a+1=l(n+1)(1\leq k\leq n, 1\leq l\leq n-1)\)とおける.
すると\(a=kn=ln+l -1\)だが, \(0\leq l -1< n\)より\(k=l\). すると\(k=l=1\)より\(a=n\)がわかる.
\(\gcd(x,a)=n+1,\gcd(x,a+1)=n\)のときも同様にすると\(a=n^2-1\)がわかる.
よって\((a,b)=(n,n^2-1),(n^2-1,n)\).
問4
感想
難しいような簡単なような…
いろいろな方法がありますが思いつかないと難しいでしょう(無難なコメント).
構成も意外と出てこなかったりしそうです.
解説
図のような感じで塗り分ける.

駒が通った道筋を辺とするとき
●から出た斜めの辺の本数=○から出た斜めの辺の本数
●から出た斜めの辺の本数\(\leq 2\times\)(●の数)=\(\cfrac{(n-1)^2}{2}\)
○から出た辺の本数\(\geq 2\times\)(○の数)\(-2\)=\(\cfrac{(n+1)^2}{2}-2\)
○から出た斜めでない辺の本数
=○から出た辺の本数-○から出た斜めの辺の本数
\(\geq\cfrac{(n+1)^2}{2}-2-\cfrac{(n-1)^2}{2}\)
\(=2n-2\)
構成は略します.
別解
こちらのサイトに別解と構成があります.
こちらのほうがきれいな感じがします.
JJMO本選2019問4 | 凸レンズの部屋(仮)
問5
感想
5番の割にはそんな難しくない気がします.
JJMO, なんで3年連続で5番にGをおくのでしょうか???
解説
学校の後輩が天才的な解法を見つけてくれたので書きます.

\(\odot AMC\)と直線\(AN\)の交点を\(P\)とおくと, 簡単な角度計算で
\(\triangle NHA\sim \triangle NMC\)
\(\triangle KAN\sim \triangle PCN\)
がわかるので
\(四角形KAHN\sim 四角形PCMN\).
すると対応する角度が等しいので
\(\angle AKH=\angle CPM\)
すると円周角の定理より
\(\angle AKH=\angle CAM\).